DIY Current Monitor on Raspberry Pi. My power calculation isn't accurate. Help please?

david0 · 9 February 2020 05:24

Hi there,

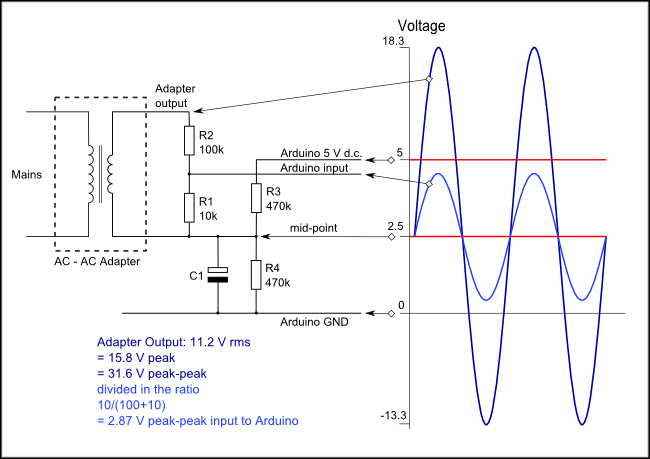
I’ll try to keep this post brief and to the point. I’m currently building a home power monitor using a Raspberry Pi Zero W and the circuit diagrammed here: Learn | OpenEnergyMonitor. My circuit uses 20 ohms for the burden resistor between CT leads. I’m in USA and I’m using a 120V 60Hz AC circuit for testing.

It is functional, but when I calculate the load of the conductor my CT sensor is monitoring, it doesn’t match the load that a power meter is showing (ie, Kill-A-Watt). I put a 700W load on my test circuit but my calculations using the data from the CT sensor only show about 390W. I have measured the load using two different commercially available power meters, and it is in fact about 700W.

I have reviewed the entire OpenEnergyMonitor AC Power Theory section, which, by the way, has been a fantastic resource, so thanks to the community for providing such a valuable source of knowledge. I have an understanding of the theory, but I’m not sure where the source of error is coming from.

Here is how I am calculating the power usage:

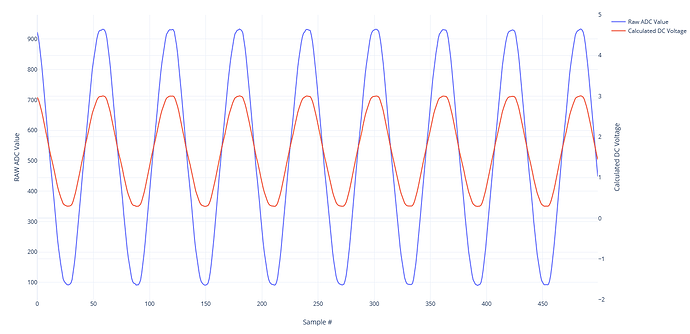
I take 120 CT sensor voltage readings as fast as the RPI can handle it, which is in between 1-2 seconds.
Find the minimum value and maximum value from the 120 readings (one value is negative, the other is positive, but the absolute value of them should be very close)
Calculate the min/max values as a percentage over/under the reference voltage of 1.6580V, or half of the 3.3V Raspberry Pi rail)
Average the two percentages to get the average peak CT reading.
The amperage is simply the percentage previously calculated of the 100A CT sensor capacity.
I assume (for now) a 120V AC source voltage, so I multiply the amperage by 120 to get the power being used.

An example with real measurements just taken with my 700W load is (I am rounding these to 4 decimals to save space below, but my program is using the full value of the floating point number):

Min and max values from 120 CT sensor readings: min: 1.6033V | max: 1.7124V
% under reference voltage: (1.658 / 1.6033) - 1 = 0.0330
% over reference voltage: 1 - (1.658 / 1.7069) = 0.03282
Average over/under reference voltage: ( 0.0330 + 0.03282) / 2 = 0.03291
Amperage on the line through the CT sensor is 0.03291 * 100 = 3.291A
Power being used = 3.291 * 120 = 394W

I’m not sure why my power calculation is low. I realize I’m not using the standard “Real Power” and “RMS Current” methods, but from my understanding the method I’ve outlined above should be working fine. Especially since the CT sensor’s output has been measured to provide linear values until saturation > 100A (on the openenergymonitor site).

Another issue I’m having is my program calculates a 0.9W load when there is no current flowing through the conductor. This won’t be a concern when I hook the CT sensor up to my house mains since I’m sure the load will always be measurable, but I am just really focused on accuracy at the design/testing stage.

Thank you for any assistance!

Edit: After reviewing my post and going back through the circuit diagram, I’m starting to think that the “reference voltage” (as I’ve termed it) is not needed in the calculations. The analog input going to the Pi/Arduino has nothing to do with the reference voltage - that’s only serving as the path to ground for the CT sensor. I’ve modified my current calculation to simply be the difference between the peak voltage measured from the CT sensor and the reference voltage. This has gotten my power calculation closer, but still not to a level of acceptable accuracy.

Robert.Wall · 9 February 2020 13:13

How are you getting analogue values into your Raspberry Pi? As far as I’m aware, a RPi doesn’t have an analogue input of any sort.

That would be my first concern. As far as current is concerned, there’s absolutely no guarantee (unless you only have pure heating loads) that the current waveform is a well-behaved sine wave, so the peak current doesn’t have to have the ‘standard’ relationship to the rms average that your other meter (especially the kWh meter that calculates what you’re going to pay for) measures.

My second concern is the rate at which you’re sampling the current wave. You live in the 60 Hz world, so one cycle of your mains lasts 16.66 ms, and you get a peak each way every 16.66 ms. You’re taking a sample somewhere between every 8.33 ms and every 16.66 ms. The awkward question: What guarantee do you have that you’ll actually hit one, or better still, both positive and negative peaks within that sampling period? This could be a major source of error.

I can’t check your numbers because you don’t say which c.t. you are using.

david0 · 9 February 2020 21:14

Robert, thanks for the reply. I left some of the seemingly important details out to keep the initial post brief. To answer your questions:

How are you getting analogue values into your Raspberry Pi?

I’m using an ADS1115 I2C ADC to get the analog input into my Pi. The ADC has an input voltage limitation of 3.3V, so my reference voltage is 3.3 / 2.

This is a great point and something I had not thought about yet. In my testing environment, I’m using an electric space heater, so I suppose the AC waveform is as close to a sine wave as it could possibly get. Does the RMS calculation method account for non-sinusoidal waveform help?

This is one of the possibilities I’ve thought of this morning after revisiting my setup. I don’t have any guarantees - I’m simply taking 120 samples in just under 2 seconds and hoping that one of them is the peak of the wave. While it’s pretty close, it’s most likely not exact. My research has led me to the idea of using a peak detector, and measuring the voltage from it instead of directly from the CT sensor. If I go this route, I’ll need a transistor gate to open and close a path to ground to “reset” the capacitor in the peak detector back to the reference voltage (and I’d also need to account for the voltage drop across the diode).

Sorry about that - I’m using the YHDC SCT-013-000 100A CT sensor. There is some uncertainty about the # of turns in the sensor. The Amazon product page shows 1800:1, but the rating on the sensor (100A : 50 mA) suggests it’s actually 2000:1, which agrees with the documentation on the OpenEnergyMonitor tutorial. I used a turn ratio of 1800:1 in my calculation for the burden resistor so that could be a source of issue too. I’m using a burden resistor value of 20 Ohms.

I’ve made a slight change in how I’m calculating power. If you do check my work, don’t use the process in the bullet points in the original post. The process I’m using now is much more accurate for my space heater, which is:

Take 120 readings from the CT sensor (< 2 seconds)
Take a live measurement of the reference voltage (about 1.6578V)
Get the max value from the 120 CT readings
Find the difference between max CT and reference. With a 700W load, the CT sensor reads about 1.7124272 V. So, the difference is 1.7124272 - 1.6578 = ~ 0.0546272 V
The difference is essentially a fraction of the maximum rating of the 100A CT sensor, so the measured current is 100A * 0.0546272 = ~ 5.462 A.
I multiple the calculated current by a constant 120V to get power. 5.462 * 120 = 655W.

I think my burden resistor value might be off by a couple Ohms because of the confusion over the turn ratio. The randomness of the 120 samples I’m taking is the next likely probability IMO, so if recalculating and changing the value of the burden resistor doesn’t help, I’ll implement the peak detector circuit next.

As for the RMS calculations, I don’t know enough about the RMS theory to understand the impact it would have on the value. I can implement the calculations summarized in the “Arduino Maths” AC Power Theory review if that is recommended.

Bill.Thomson · 9 February 2020 22:30

Forum user ybizeul tried using the ADS1115 only to find out its max sampling rate (860 SPS)
is too slow. Here’s the thread:

There are several threads on the forum about the ADS1115.
This should help show why the ADS1115 isn’t suitable:

david0 · 9 February 2020 23:00

Bill, the threads you linked are very helpful. Thanks. I wasn’t aware the 1015 had a faster sampling rate than the 1115.

Even still, is the 860/s sample rate not fast enough for measuring a 60Hz AC wave? Here’s my thinking:
If a single wave completes one oscillation in 1/60th of a second, that means the crest and trough of the wave happen every 1/120th of a second. With a maximum sample rate of 860 per second, I should be able to capture the peak, trough, and about 7 samples in between each oscillation, right? Is that not enough resolution to accurately calculate power usage? This of course assumes I can get the maximum sample rate out of my board (Pi Zero), which I may not be able to. Maybe I’ll try with a Pi 3B+ and see if there’s a difference.

I’ll order the 1015 ADC to compare it to, and if I don’t end up using it, I’m sure it can come in handy for something else in the future.

I’m beginning to understand now that in order to accurately calculate the power usage, I need to have an accurate sample of the waveform. Calculating the usage based on the peak voltage per cycle is not accurate, so the idea of using a peak detector won’t help my scenario.

Robert.Wall · 9 February 2020 23:04

In this post is @dBC’s favourite picture of a distorted current wave:

The rms value of an alternating wave (in your case current) is the direct current that would produce the same heating effect in a resistor. Consequently, it’s the most widely used measure of alternating waves.

It not only helps, it gives an accurate measurement that is universally recognised.

That rubbish has resurfaced? The ratio of a c.t. is always defined as a ratio of currents, never turns (not the way I learned my electrical engineering anyway). A 2000:1 c.t. is suitable for measuring 2 kA using a 1 A ammeter as the burden. That’s whole lot bigger and heavier beast than an SCT-013-000.

In all honesty, I’m with Bill here. Give up trying with the ADS1115, it’s simply not fast enough to measure a 60 Hz wave, let alone get a reasonable value for the current in dBC’s picture.

Bill.Thomson · 9 February 2020 23:06

Popular picture!
That’s the one I referenced as well.

david0 · 9 February 2020 23:18

I see, thank you. I will drop the peak-based calculation technique I put together and replace it with the RMS method. In theory, I suppose I should be able to somewhat accurately calculate the power consumption of my space heater using my current calculation method since it’s a resistive load, but I understand why this won’t work for more complex electronics.

I ordered the ADS1015 and it will be here tomorrow - I suppose I have some time until then to at least play around with the 1115 and see if the Pi Zero is even capable of processing 860 samples per second.

And yes, I must have flipped the ratio around for the CT sensor: 1:1800 is what I meant (and what the product page shows). So if we look at the ratio of currents printed on the CT sensor itself, 100 A / 0.050 A = 2000 (NOT the 1800 the product page shows). I’ll redo my burden resistor calculation in the mean time.

I’m beginning to have a clear picture of why I was struggling. Thank you both for your help so far!

Edit: I also have a few MCP3008 ADCs in my box. Googling the sample rate for these chips shows an insanely high rate of 100+ KSPS. I suppose the obvious answer is to use this chip instead of the ADS 11x5? I suspect at this speed, I’d run into limitations of the Pi or Python itself.

Bill.Thomson · 9 February 2020 23:42

In a word, Yes!

True.
Keep in mind that’s conversion rates of up to 200 ksps. The conversion rate is controlled by the
SPI clock. The datasheet says:

6.2 Maintaining Minimum Clock Speed

When the MCP3004/3008 initiates the sample period, charge is stored on the sample capacitor. When the sample period is complete, the device converts one bit for each clock that is received. It is important for the user to note that a slow clock rate will allow charge to bleed off the sample capacitor while the conversion istaking place. At 85°C (worst case condition), the part will maintain proper charge on the sample capacitor for at least 1.2 ms after the sample period has ended. This means that the time between the end of the sample period and the time that all 10 data bits have been clocked out must not exceed 1.2 ms (effective clock frequency of 10 kHz). Failure to meet this criterion may introduce linearity errors into the conversion outside the rated specifications. It should be noted that during the entire conversion cycle, the A/D converter does not require a constant clock speed or duty cycle, as long as all timing specifications are met

david0 · 10 February 2020 00:10

Awesome. I had went with the ADS11x5 for ease of use/integration over the MCP. I haven’t used an MCP before so I’ll have to look into interfacing it with a Pi.

So the recommendation to not exceed 1.2ms polling interval is to give a hypothetical capacitor ample time to discharge?

And with the MCP3008’s 8 channels, I could, in theory, have up to 8 CT sensors and sample each channel at 10k SPS?

Given the potential limitations of the Pi that I’d run into at this speed, I’m thinking it might be better to do the sampling and low level maths on an Arduino, and then provide those measured/calculated values to the Pi. I’m just brainstorming out loud here… I have an Arduino Uno but I’m not familiar with its hardware limitations or how I’d connect it to the Pi. I am focused on the Pi only because I’m already deeply familiar with Linux, networking, and Python.

Robert.Wall · 10 February 2020 00:54

Not quite. The capacitor they’re referring to is the sample & hold capacitor inside the ADC, and the idea is for it not to discharge while the S & H conversion is taking place. Hence, you mustn’t go too slowly while reading it. But you can of course pause between reading a sample and commanding it to do the next one while the Pi processes the numbers.

I don’t think so. There’s only one ADC, so you can read one channel at 10 ks/s, or 8 channels at 1.25 ks/s each - less I suspect because of the time taken to switch the input multiplexer.

In theory, you need at least two samples per cycle at the highest frequency you’re interested in. I think a general consensus is you don’t need to go higher than 2 kHz, which implies a sample rate of 4 ks/s. Using the ADC in the Atmel 328P in free-running mode, that will do about 9600 s/s, so if you want to measure current and voltage of one feed, to give you real power, you’d have 4800 sample pairs per second, or 80 sample pairs per cycle, and that should be good to way beyond the highest harmonic you’ll come across.

You won’t get that using analogRead( ) - emonLib uses that and you’ll get about 44 sample pairs per cycle.

What you have there is very close to an emonPi, and all the information for that is here, either in the Guide or the Wiki.

EmonLib and emonLibCM will both run on an Arduino Uno, using our standard sketches (but with the RF module stuff removed, of course, and using serial comms to the RPi as per the emonPi).

david0 · 12 February 2020 01:43

Here’s an update on my progress. I implemented the MCP3008 chip today and started playing around with clock speeds. I had some trouble at first, but after verifying my circuit to read the chip, I remembered the tip that @Bill.Thomson pointed out from the datasheet about the minimum clock speed. Thanks again Bill - that totally saved me a huge headache. I’m currently trying to find the sweet spot between granularity and the amount of data needed to process.

Here’s a plot of data I’ve gathered using Python (spidev) and the MCP3008 at various clock speeds.

20 kHz (blue) is decent (probably better than what I was getting with the ADS1115), but looks choppy to me. 200 kHz is very accurate but 100 samples for a single oscillation (equivalent to 6000 SPS) is extreme overkill for my needs! 100 kHz still looks pretty good too, but then again, the load is an electric heater so the wave should look nice regardless. I’ll have to see how the wave looks when charging a laptop or something of that nature.

I have not yet played around with multiple CT sensors on the MCP 3008. When I get to that point, I’ll start building the framework for a threaded Python application to probe the different analog channels on the MCP simultaneously.

Edit: I forgot that I wanted to add the speeds I’m getting with the MCP3008. I’m collecting 4150 samples on a Raspberry Pi 3 B+. The time to collect this many samples at the specified sample rate are below:

20 kHz : 8.93 seconds
50 kHz : 3.43 seconds
75 kHz : 1.98 seconds
100 kHz : 1.64 seconds
200 kHz: 0.6846 seconds

Here is a plot with samples taken at 50 kHz and 75 kHz.

To my untrained eye, 75 kHz might be the right spot. The sample quality clearly starts to deteriorate at 50 kHz.

Bill.Thomson · 12 February 2020 01:47

YVW,S!

Actually, the 20 kHz sample is still fairly well distorted, i.e. read that as “bad.”
The 100 and 200 kHz samples look much better.
Try it at say, 50 or 75 kHz.

Bill.Thomson · 12 February 2020 02:14

You’ve got a little flat-topping (on the +ve peak of the first cycle)
and a little bit of a “divot” (just before the third +ve peak)
There’s a little flattening on the -ve peaks too.
But overall, it looks better than the sample at 20 kHz!

david0 · 12 February 2020 07:15

I’m stuck on calculating the RMS voltage (in theory). I’m using this circuit (source) with a 3.3V DC board voltage and a 1.65 reference voltage for my AC input.

My ADC is 10 bit so it returns values between 0 and 1023. Here is a sample of the analog data I’m getting from the circuit as read by my ADC:

I am having trouble finding the RMS voltage from the sample data series. I can turn the raw data into actual voltages being fed from the circuit no problem, but… then what?

With the current transformer, it was easy - I knew the input/output ratio and could apply the ratio to my calculations. I’ve calculated the input/output ratio of my AC transformer by measuring the input and output voltage. The ratio is 11.5:1.

I don’t know if it’s because I’ve been at this for many hours today, but I just can’t seem to figure it out on paper. I think there are two ratios at play - one for the AC transformer and one from the input signals that are conditioned from the circuit. Maybe the problem is I haven’t determined what the peak voltage output of the AC transformer is?

Edit: I should add that my intention in using the AC transformer is to measure voltage at the start of each “polling cycle” where I will calculate the power usage using the CT sensor data for that cycle. Instead of assuming a constant 120V in my application, I just want to probe the AC transformer and get a “live” voltage reading that I can then use for the next second or two while I conduct the calculations (as opposed to calculating the instantaneous voltage for each data point).

Robert.Wall · 12 February 2020 13:48

I’d read the data sheet very carefully before you spend too much effort on that - look particularly the block diagram on page 1. That shows a multiplexer on the front end of a single ADC, so read what I wrote above again.

If it’s any help, emonLib on a Atmel 328P manages about 44 samples per your US cycle, if you have regulations regarding the maximum amount of harmonics you’re allowed to inject into the supply, then that’s a good guide to the sort of maximum frequency you need to resolve. If the law says there must be negligible current at (say) the 15th harmonic, there’s little point in trying to measure it in the first place.

You’re right, there are. The mains voltage is divided down twice, once by the transformer (in the ratio you’ve measured at 11.5:1) and then further by the resistive divider chain R1 & R2 in the ratio 10k / (10k + 100k), or 11:1 So the overall ratio is 126.5:1

That’s only important to ensure you’re not exceeding the input range of the ADC. As long as you use consistent units throughout, it makes no difference to the ratios. I have a ‘rule of thumb’ - the input voltage needed at the ADC is 1.1 V rms, for a 3.3 V input range. That takes into account component tolerances and allows a bit of headroom. If you design the voltage divider for that but no more at your maximum supply voltage (resistors and transformer combined, and it works for c.t. and burden combined too) then you won’t be far wrong.

You won’t get accurate power readings for loads like induction motors, or computer power supplies or the like, doing that. You’ll be calculating apparent power, not real power which is the one you pay for. Apparent power is equal to real power only with a purely resistive (heating) load. For everything else, it’s always greater. For something like a microwave oven on standby, it will probably be many times - 10 or so - greater.

david0 · 12 February 2020 18:47

I’m thinking that if the chip can read up to 200k SPS, and I’m only sampling the CT sensor at about half of that, there is some leftover read bandwidth in there. I would anticipate some latency when changing the channel to your point… my threading idea would essentially have to set the channel upon each sample, so I wonder what that would do to the effective read speed. I’m getting ahead of myself with that though

Looking here at the math theory section on the guide… to calculate real power, you need instant current and instant voltage. The instant voltage is essentially the net change in input voltage * the overall ratio? For instance, the initial raw ADC value in the voltage data I gathered above was about 900. So, the net change in DC voltage when ADC input = 900 is ((900 / 512) - 1) * 3.3 ~= +1.25 V over the 1.65V reference voltage. And the instantaneous AC voltage at that point of the wave is 1.25 * 126.5 ?

I see, thanks. Looks like I need to modify my program to take one CT sensor sample, change ADC input, take one voltage sample, change back to the CT sensor input, and repeat. It will be interesting to see the impact to sampling speed when I change channels before every sample. I also thought about using another ADC on the Pi’s second SPI bridge to read a single channel from each one simultaneously (via threading), but I’m not sure which one would be better. Unfortunately I don’t have any hands-on time to work on the project today so I’ll have to revisit it tomorrow.

Thank you for the feedback! You rock

Robert.Wall · 12 February 2020 21:13

What I’ve done in emonLibCM is, for each of the inputs, as each sample is read I subtract a nominal offset (which is hopefully the inputs’s quiescent value but we know it never is, exactly), then accumulate the resulting value and the resulting value squared, and for each pair of voltage and current samples, V × I.
Then, at the end of the averaging period, calculate the averages and subtract a final correction for the offset, taking advantage of the relationship for the components of a complex wave:
[rms of signal+ offset] = √ (signal² + offset² ).
For the real power, it is only necessary to subtract the product of voltage offset and current offset (the ‘offset power’) from the average power (the average of the instantaneous powers).
The nominal offset is subtracted first only to keep the numbers smaller. There’s no other reason to do so. Doing all the ‘per sample’ maths as integers speeds up the processing significantly.

At this point, the squaring and offset removal processes have removed the need to know the midpoint voltage, and you simply apply the scaling factor for the number of volts input per count out of the ADC. So if your ADC is 4096 counts per 3.3 volts at the ADC input, and your voltage divider is 126.5 V at the mains input per volt at the ADC input, then overall it’s 4096/3.3 counts per 126.5 V at the mains input.
It’s exactly the same process for current.

If you want real power accurately, another demon rears its ugly head - phase errors. Your c.t. and your v.t. have a phase error - the output waveform is out of step with the input wave, by anything up to a few degrees. Usually, the output appears to be ahead of the input (it leads). You can get an idea of how much from the test reports I did for the ‘Learn’ section. What that means is, as you’re sampling quite fast, you’ll need to delay one set of samples by the difference between the phase errors of the two transformers. Using our standard ones as an example, the v.t. shows a lead of around 5°, and the c.t. shows a lead of about 4°, so you’d need to delay using the v.t’s readings by 1°, or 46µs, and at 200k SPS (100k sample pairs per second), that’s 4.6 samples. And that needs to be adjustable, because the phase error is different for each type of transformer, and it varies according to what’s being measured.

There’s no real advantage in doing that, as you now know. I don’t think you’re that desperate for a high sample rate.

david0 · 13 February 2020 17:16

Thanks for the breakdown. This is what I’m currently doing to find the RMS current since I’m taking all the current samples at once. When I refactor my collection function to take one sample of each channel (current sensor and voltage sensor), I’ll follow suit. The nominal offset/quiescent value is simply the reference voltage in the signal conditioning circuit (~ 1.65xxxV), right? Or approximately 512 (one half of 1024) from the raw ADC channel?

I think I follow this - but I’ll have to get back to you later today when I am back in front of my project to see if I’ve ironed this part out.

This is absolutely fascinating to think of. I’m not an electrical engineer, but I do like thinking programmatically, so here’s how I would attempt to correct the phase drift between inputs. Is this correct?

Analyze the samples and look for the first peak (or trough) in both the current and voltage samples.
Assuming the samples are in an ordered list, grab the index position of the initial peak for the CT and V samples. Find the difference between the two indexes, and this is equal to the number of samples that the two sets are out of phase by (let this equal F)
Align the two sets by removing F number of samples from the set that peaks after the first, so that the peaks begin at the same index position number in their respective lists. Also remove F number of samples from the end of the set that that was previously untouched, so that the total number of samples in each set is the same.
Do a couple spot checks throughout the sample data to ensure the peaks (or troughs) are still aligned. (Is this even necessary? Can/does the AC frequency from a large-scale commercial energy provider ever slightly drift away from 60Hz? Or is my initial peak alignment method accurate enough for correcting the <1 second worth of sample data?)

Here’s a marked up chart of what I mean using my sample data. This sample data is not actually the voltage and current samples - it’s just the data I had readily accessible. It is actually two different current samples taken at different sampling speeds (so the wavelengths of these samples aren’t even the same and they’ll never align). But, for the sake of theory and demonstration, suppose these two waves were sampled at the same rate and this was an actual variance between my CT and voltage sensor readings.

In summary, I would shift the blue wave sample data left by 21 positions so that its peak aligns with the peak of the purple wave. I would then remove 21 samples from the end of the purple data set.

Robert.Wall · 13 February 2020 17:48

Correct.

You cannot solve that in a program - or you can, but only when you know that current and voltage are exactly in phase. The whole point of measuring real power is the type of load shifts the relative phases, and that’s what you measure (or rather, you measure the effect of them shifting).
The easy and practical way to do it is fix yourself up with a big purely resistive load - water heater / electric kettle / fan-less electric heater etc, and tweak the one set of samples backwards and forwards until the get a maximum power - or better real power ÷ apparent power (V × I) = 1 - or as near as you can get it.
You can’t rely on the positions of the peaks nor the zero crossing points, because distortions in the transformers move them about, and it’s the 60 Hz component only, stripped of all its harmonics, that you’re bothered about.