The importance of continuous sampling

[dBC]

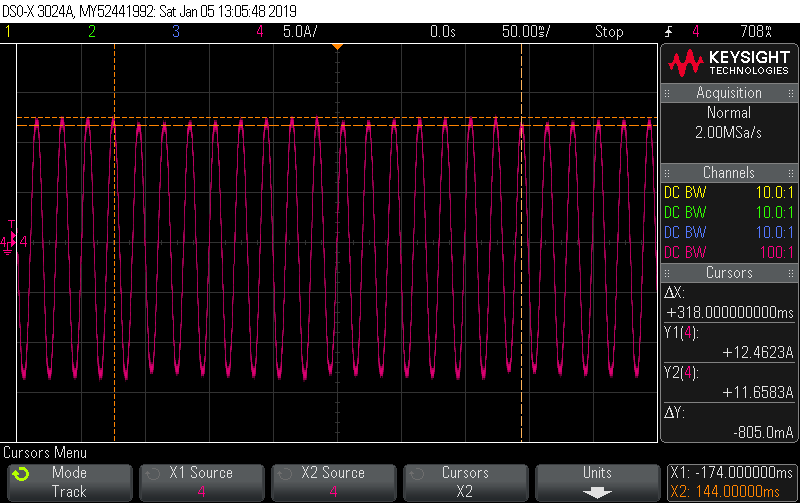
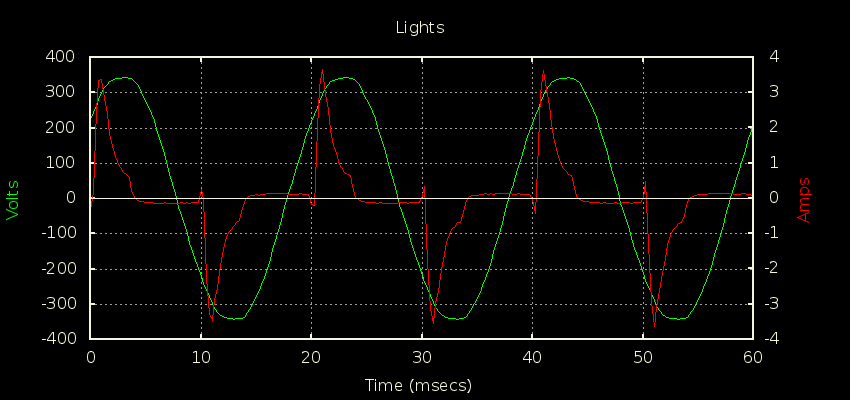
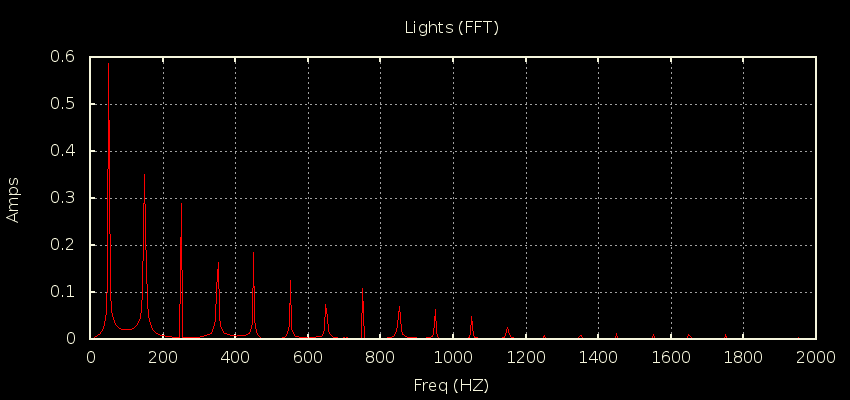
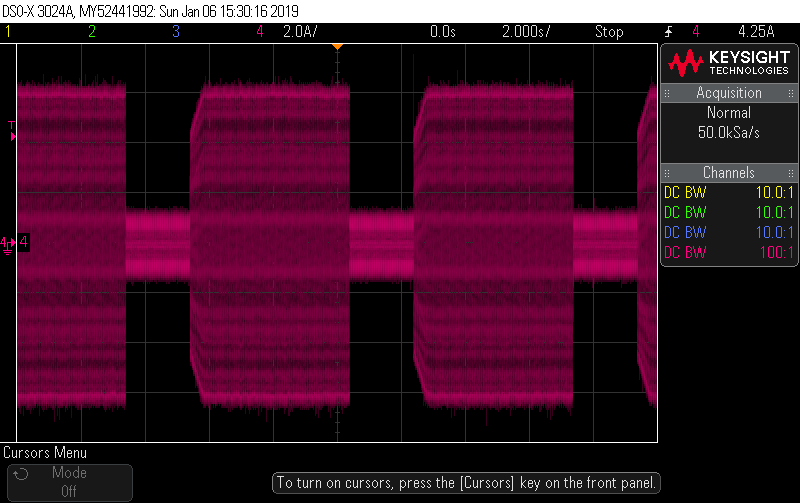
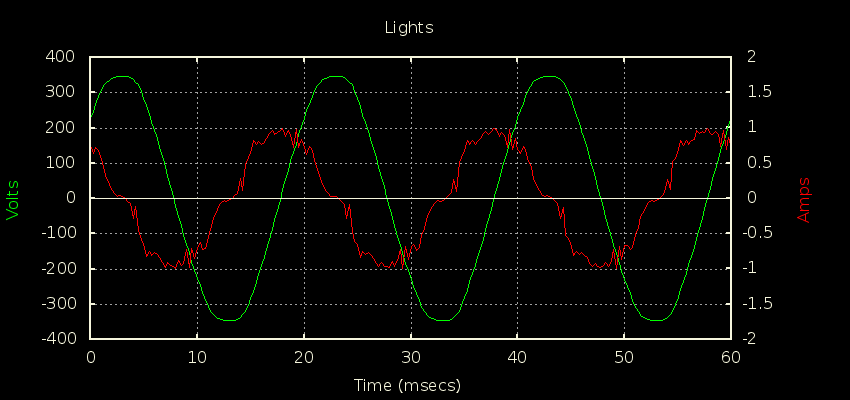
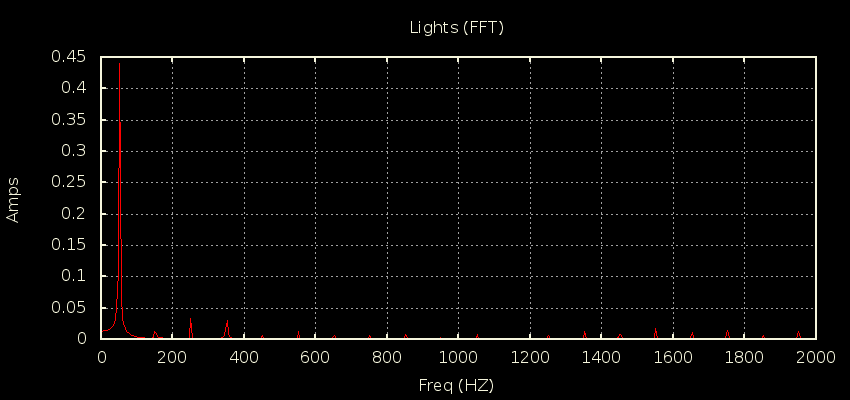
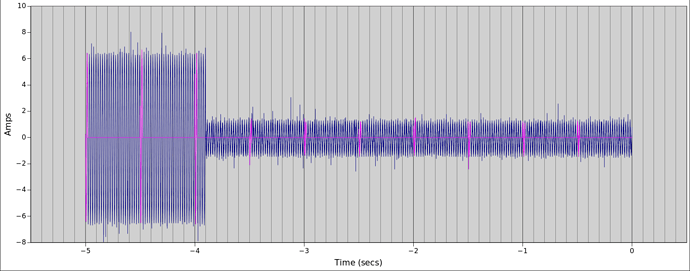
I got a chance to put a scope current probe on a 2200W induction hob recently to see for myself why it’s often quoted as an example of a load where true continuous sampling is required for decent accuracy. You can see just how much the current draw changes from cycle to cycle here:

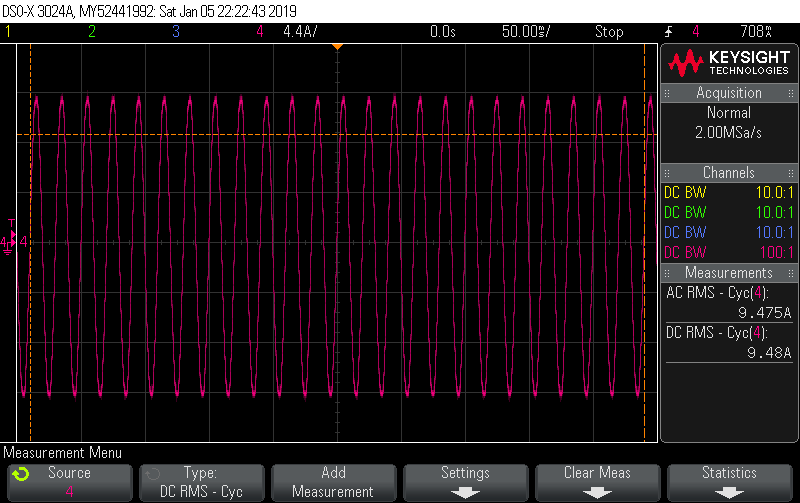
There’s close to 7% variation in cycles in this snapshot of 25 cycles, with the lowest having a peak of 11.658A and the highest a peak of 12.462A. If you’re doing true continuous sampling then this is a pretty unremarkable load to measure; it has very little distortion and almost no phase shift giving it a unity PF to two decimal places. It’s as easy to measure as a 2200W resistive load.

If on the other hand you’re doing “round robin” sampling, whereby you intensively sample one channel for 2 or 3 cycles, and then assume the signal is the same for the next half-second or so as you sample the remaining channels, you run the risk of some significant errors creeping in, all depending on the luck of which 2 or 3 cycles you picked up. And in this case it’s a significant load, the old motto of “big loads are easy to measure” doesn’t always apply if you’re not doing true continuous sampling.

In an ideal world you’d have a dedicated ADC for each channel, and that’s how the pro energy ICs work. If that’s out of reach then a close second is to step through the channels on each sample. Provided your sampling rate is fast enough for the job at hand, you’ll still get enough bandwidth out of each channel and you won’t have any half-second deaf periods where you’re not looking at the signal at all. I believe that’s how Emontx3-continuous and the new EmonLibCM V2 both work, and it’s also how the stm32 example code works. I think that’s a step in the right direction for improved accuracy.

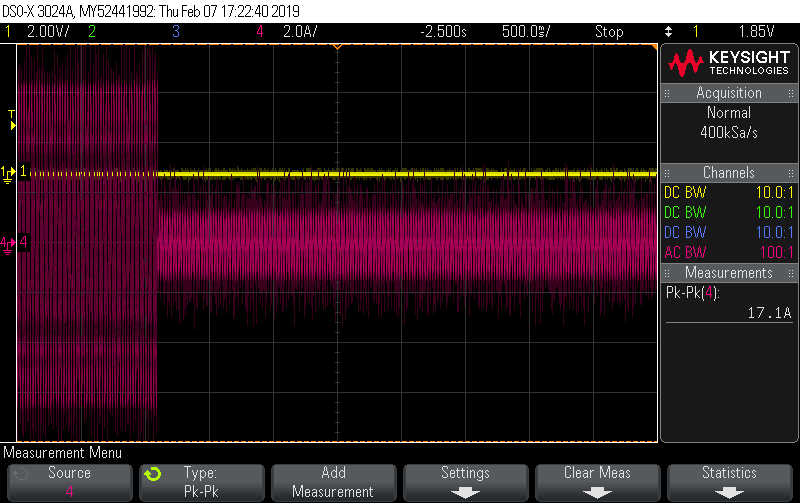
By comparison, here’s the same set up as above but measuring a simple electric kettle of roughly the same wattage. In this case you can see each cycle is pretty much an exact replica of the cycle before it, so the assumption that the signal will be the same for the next half-second or so is a fairly safe one, regardless of which 2 or 3 cycles you measured.

[Robert.Wall]

@dBC

I believe that’s how the new EmonLibCM V2 works

Your belief is correct.

[TrystanLea]

The original comment here by Overeasy has been removed as it breached our code of conduct.

@dBC clarified below that this thread was not written in reference to IotaWatt, it was aimed to contribute instead to the application of continuous monitoring firmware on the EmonTx and continuous monitoring firmware development for the STM32 platform.

[dBC]

Actually, my motivation was to re-enforce continuous monitoring as a design goal in the stm32 stuff. I was originally going to post the pic in that thread, but then figured it was a generic enough topic that all meter designers might benefit. A secondary motivation was to commend EmonLibCM V2 for going that route.

@overeasy

although the author has not actually looked at how that (IoTaWatt) works

Indeed… until your post now I would have assumed it does do continuous monitoring. Is there any reason why it can’t?

@overeasy

760 sample pairs per cycle

Since you raise it I think that makes for a very good case study in the point I was trying to make. The design decision here is how to best use an impressive 38,000 samples/sec sampling rate. You can either point it at all at one channel and then move onto the next, or you can share it amongst your channels on a sample-by-sample basis.

You seem to be operating under the mis-conception that the faster you sample a channel, the more accurate the result will be. In fact, the faster you sample a channel the higher your bandwidth will be. Regulations restrict how much energy can be in the higher harmonics. Typical revenue meters (and the energy ICs found inside them) have a bandwidth of around 2 kHz, yours is closer to 20kHz. If you point all of that sampling horsepower at a single channel, you’re doing a huge amount of maths for no change in the result.

As a general rule I think you’d get much better results if you spread that horsepower across your channels. Then all the maths would be doing something useful instead of doing something that adds up to ~0 (energy above 2kHz). I say general because I don’t know enough about your architecture to know if that’s feasible. If it is, you may want to consider it, if not keep it in mind for your next version.

[dBC]

To illustrate the “lots of maths that adds up to zero” point, I’ll dust off the pic of my most distorted channel made up of a boat load of CFLs:

My monitor measures that out to 2kHz:

Each of those blips represent a bit of energy that needs to be measured, although a lot less than it appears in the graph. That relatively large blip at 150Hz for instance gets multiplied by the equivalent 150Hz blip on the V signal which is much much smaller because V is typically much less distorted. So all those blips (bar the first) get seriously dampened once you multiply them by their corresponding V blip at that frequency.

With that V attenuation in mind (but not shown), you can see there really is not much to measure by the time you get out to 2kHz - even without the attenuation there’s bugger-all out there. With your 38000 samples/sec your equivalent graph goes all the way out to 19kHz, so you’re really just adding in a whole bunch of zeroes.

[dBC]

The other challenge it presents for monitors not doing continuous sampling is fairly rapid “thermostat” cycles. In this pic it’s Off for 2 seconds, ramping for 0.5 seconds and on for 4.5 seconds.

[dBC]

@dBC

Then all the maths would be doing something useful instead of doing something that adds up to ~0

Like watching what the induction hob is doing. The problem with only looking at 1-in-25 cycles and relying on the law of large numbers to eventually get you to the right answer is that it assumes the signal is constant. In the case of an induction hob that’s not a safe bet.

[Robert.Wall]

@dBC

In the case of an induction hob that’s not a safe bet.

It’s been recognised for at least as long as I’ve been associated with OEM that the “discrete sample” method is adequate when conditions are changing relatively slowly, but there are serious limitations with loads that vary rapidly. And it is with the sort of load that you mention (and I include in that the halogen type of hob), that was foremost in my mind when advocating the concept of continuous monitoring.

Clearly one sample every half-second is a significant ( ×2 ) advance over 200 ms every 10 s taken over a long period, but even so, it’s a lottery as to whether the correct value is recorded during any half-second interval, or how much is under or over-recorded, especially when the switching rate converges towards the sample rate.

[dBC]

Yes, I’d often heard it quoted in here, but never quite knew the reason why. Nothing like a few scope pics to hammer the message home. It also revealed the cycle-by-cycle changes this particular one makes as it’s ramping.

These 4-burner hobs are getting pretty popular in these parts. I’m told that once you get one, your old electric kettle goes in the bin so these things get powered up every time you make a cuppa’, and end up a fairly significant contributor to your total energy bill.

[Robert.Wall]

@dBC

It also revealed the cycle-by-cycle changes this particular one makes as it’s ramping.

That came as a bit of a surprise to me. I guess the reason that’s done - and it must be deliberate - would be to minimise the perceived effect of any flicker that it induces on a weak supply.

[dBC]

I wonder if it might be doing some sort of pot-detection? There’s heaps of info in AN2383 if anyone wants to build their own. I’ve only scanned it briefly, but I did notice stuff like:

This causes the system to have an oscillating resonant frequency strongly dependent on the type of pot placed on the plate at different times.

Therefore the 9 working levels cannot be based on constant frequency levels. The PWM
frequency must be adjusted to the selected level in order to work with the pot placed on the
plate at that moment.

So each working level does not work on a constant PWM frequency, but a constant current.
By reading the I-CTRL feedback signal, the MCU smoothly adjusts the PWM frequency in
order to keep the current constant for the selected working level.

[Robert.Wall]

@Robert.Wall

I guess the reason that’s done - and it must be deliberate - would be to minimise the perceived effect of any flicker that it induces on a weak supply.

Thinking about it, that’s probably wrong, because it would also need to ramp down to hide the effect of flicker.

[dBC]

The standby current on this thing is a shocker: 0.66A just sitting there waiting for someone to press a button. 3W Real and -165 VAR Reactive, PF of 0.018.

[Robert.Wall]

No prizes then for guessing how they’re deriving the low voltage to run the bit that detects the button being pressed. I presume the h.f. mush on the current wave is what’s getting through what is effectively a high pass filter. It would be interesting to see how the Fourier analysis of that will look compared to the one in post no.5., and how far up the frequency spectrum it stretches.

But in fairness to the title of this thread, continuous or discrete sampling would make little difference in this case.

[dBC]

Well spotted, it does indeed go all the way out to 2kHz and potentially beyond. I vaguely recall that really low power devices (< 5W maybe?) are exempt from the harmonic rules.

[Robert.Wall]

Yes, you’re right. Both here and in the USA, and I presume that’s common elsewhere.
Here, lighting equipment with power not greater than 25W is exempt. Otherwise, for the 3rd harmonic, its 3.45 A for portable tools, and 30 × power factor for lighting, and 2.3 A for almost everything else, but the limits fall with the harmonic order and are specified up to the 39th - near enough 2kHz.

I’d be surprised though if that (microwave?) device is actually generating those harmonics - I’d suspect that they’re on the supply and the capacitor dropper is acting as a low pass filter and allowing you to see them being conducted to neutral as a current wave. If you have a suitably rated capacitor and resistor, which could not possibly generate harmonics, to hang across the supply, that would be a revealing test.

[dBC]

This is still the same induction hob, which now well and truly replaces the microwave as my most current-hungry appliance in standby. Unfortunately I don’t have the bits required for your suggested experiment, but will try to remember to pick them up next time I’m ordering something.

[dBC]

@Robert.Wall

it’s a lottery as to whether the correct value is recorded during any half-second interval, or how much is under or over-recorded, especially when the switching rate converges towards the sample rate.

I got to wondering how to go about quantifying that in some way. I think everyone agrees that it’s really only relevant when the load is changing rapidly, but when the load is changing rapidly the 5-second interval average power is changing wildly from reading to reading as well. Comparing to a reference meter isn’t a lot of help because you’ve no way of knowing if the reference meter and the meter under test are sync’d to the same 5 second interval. You really need the two meters looking at the exact same 250 linecycles and then compare their results.

There’s no way I can tell my energy IC based monitor to only look at every 25th cycle, it’s just not in its DNA, but the emontxshield+stm32 demo code offered some possibilities. I modified the f/w slightly to base everything on ZX detected half-cycles and configured it for 500 half-cycle (5 second) integration. Then I pointed two channels at the induction hob to see how they clocked it:

Ch1 W     Ch2 W      Diff
566.81,  567.46,    0.11%
550.16,  551.06,    0.16%
192.38,  192.96,    0.30%
388.26,  388.87,    0.16%
561.32,  562.03,    0.13%
378.93,  379.65,    0.19%

All pretty good so far and you can see the wild variations from one 5-second interval to the next as the hob does its thing. 0.3% was the biggest discrepancy I saw.

Next, I knobbled Ch2 to only look at every 25th cycle - so just 10 cycles over the 5 second integration integral. That gave:

Ch1 W     Ch2 W      Diff
190.64,  195.24,    2.41%,
416.40,  473.19,   13.64%,
552.16,  568.24,    2.91%,
347.01,  288.47,  -16.87%,
217.29,  287.87,   32.48%,
553.96,  565.81,    2.14%,

So in one 5 second interval the reported average power was out by 32% (I actually saw 40% at one stage, but didn’t have the scope configured to capture it, so went with this run). Next I toggled a spare IO pin whenever the error exceeded 30% and used that to trigger the scope, which was configured to capture 5 seconds of current prior to the trigger (trigger is just off the right edge). That produced this:

In broad-brush terms it’s 1.1 secs of high power, followed by 3.9 secs of low power.

The final step was to extract that data from the scope and highlight every 25th cycle:

Even broad-brush you can see what’s happened. Ch2 saw a 3/10 ratio of high:low while Ch1 saw the correct ratio of 1.1/5 and those ratios come out pretty close to the 32% error reported above.

Now if you let it run long enough even that under-sampling eventually converges on the correct result but it takes a while. Even over the 30 seconds of those 6 consecutive 5-sec reports above, Ch2 was over reading by 4.45%. At those timescales there’s a real risk that chef will have bumped the hob up or down a notch and then you’ll be busy chasing a new target without ever converging on the old.

This also demonstrates why metrics like “long-term agreement with the revenue meter to within 1%” shouldn’t give you much confidence about the accuracy of individual power readings. In this case my Ch2 was out by much as 32% (actually 40%) and yet I could still meet the long-term 1% agreement with the revenue meter, provided chef was agreeable.

[overeasy (Inactive)]

So this thread starts off trying to make a point using a fairly steady state plot of an induction cooker that has a stated 7% or so variation cycle to cycle. By observation, it’s not at all random, but rather is a sawtooth pattern as evidenced if you look at the bottom of the traces.

The period is around 7 cycles. My assertion was that random sampling of those variations at about two per second would flesh out the average to less than 1% over a reasonably short time frame. That argument was deemed offensive and removed, but apparently the point was taken because the follow on argument uses a new set of samples where the appliance now “thermostats?” from second to second.

The new argument is that this will not stand up to statistical scrutimy of random sampling. Lets take a look at that argument.

First, the analysis is based on the premise that the sampling is strictly periodic - one every 25 cycles. That is incorrect. The sampling is for intents and purposes random. There are 100 opportunities (zero crossings) per second to start a cycle sample and there are many asynchronous events in the subject device that can cause it to skip a half cycle. Moreover, that is only in a fully loaded device. The sample rate can be as high one in three cycles.

Now looking at the trace from above:

How convenient. The trace covers 5 seconds. That’s 250 cycles. The non-random samples have a period of 25 cycles. 250/25 = 10.000000. So this is not even close to a representation of a random event. Sure, there are three “samples” in the high power zone, and 7 in the low power zone. Take a close look. How hard is it to do that?. How many even modestly random samples do you think would ordinarily occur during that 1.1 seconds? Let’s see:

The 1.1 second trace represents 55 cycles. In order to get three samples into that block at 1/25 the first one would need to be in the first 5 cycles, so in a random world, probability says that would happen 20% of the time.

So 20% of the time 30% (3 of 10) would be high, and 80% of the time 20% (2 in 10) would be high. When you blend that you get 22% of the samples will be high, which is the exactly what the scope trace shows - 1.1/5.

That’s why even with a relatively short time interval, the above experiment started to converge. But it was skewed in that it used a rigid fixed interval rather than a somewhat random interval. And I’m not really buying the argument that the chef will change the game every 30 seconds as a “real risk”. That’s may be a little hyperbolic.

As these arguments go, there will no doubt be another run at it with a more obscure fringe case and again, cherry picked data. When my original post was censored, it was probably because I pointed out that these guys make a lot of arguments with oscilloscope traces and convoluted analysis. I’m just saying be wary of false assumptions and cherry picked data. When I talk about a “practical example” of a problem, I mean compare the actual results from the device in question with a reliable standard, using a reasonable common load. I don’t buy the argument that folks are getting bad numbers, they just don’t know it. Is it just me or is that king naked?

[Robert.Wall]

@dBC

You really need the two meters looking at the exact same 250 linecycles and then compare their results.

Or, you have to go back to basics and think what the root mean square average (when considering voltage or current) or the average (when considering power) really means. It’s the value that gives the same heating effect that a steady quantity of the same numerical value gives. And to make the average meaningful, the averaging period must either be “long” compared to any cyclic event, or perfectly synchonised to it - which is what your “two meters” implies.