Having an oversized heat pump, I recently wondered whether the high flow rate pump that goes along with it might also just be too much. Typically, everyone wants a high flow rate but at some point the electricity consumption of the pump will also become significant…the question is when.
To find this optimum, let’s have a look at what goes into it. We have our design heat loss P_heat and our radiators (or generally emitters) are chosen so they deliver this power into the house when they are at a specific temperature T_rad. Typically, this temperature is approximated as the mean of flow and return temperature, so T_rad = 1/2 (T_flow + T_return). Together with the mass flow heat equation, we can express the required flow temperature to reach our radiator temperature given a specific flow rate:
T_flow = T_rad + P_heat/(2 c flow_rate)
We see that the flow temperature is at least as high as the required radiator temperature, with an additional offset proportional to the required heating power and inversely proportional to the flow rate. For my house with 30°C radiator temperature (0°C outside) and heat loss of around 3 kW, the flow and return temperatures vs. flow rate look like this:
As flow rate increases, the flow and return temperature asymptotically approach the required radiator temperature, which would result in lower compressor electricity use due to higher COP at lower flow temperatures. If pumps didn’t need power, infinite flow rates would be best.
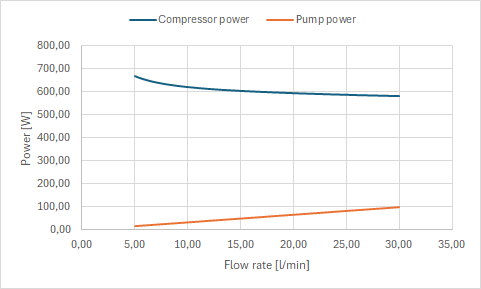
However, the required electrical power of the pump increases with flow rate. It appears this goes with the cube of flow rate, but I can’t confirm this. For simplicity I used a simple linear relationship that I approximated from my system’s pump, but the analysis works for more complex cases as well.
There were quite a few discussions on the forum how much of power put into the circulation pump ends up as usable heat in the house. For the sake of this analysis, I have assumed that all the electricity going into the pump is converted into heat. Here we can see how required compressor power decreases (due to increasing COP with lower flow temperatures) as pump power increases. The total heat being put into the house is constant. I did a simple linear approximation between compressor COP and (T_flow-T_outside) based on my Vaillant’s datasheet to get the compressor COP.
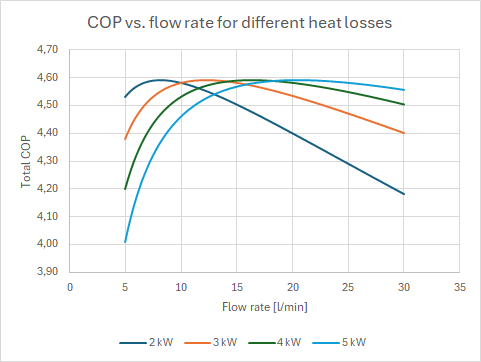
Adding those two up and dividing the required heat power by the sum gives us the total COP of the whole system. The next graph shows this for different total heat loss scenarios.
We can see that there’s an optimum point where we achieve the best possible COP. The higher the heat loss, the higher the optimum flow rate. It’s not a lot, but depending on where on the curve you’re sitting it can be up to 5% improvement. For the case that not all pump power ends up as heat and more realistic pump power vs flow rate curves, the peak will be more pronounced.
So back to my initial question - what about my oversized heat pump? My house is roughly represented by the orange line in the previous plot - 3 kW heat loss at 0°C. The optimum flow rate would be at around 12.5 l/min - which is lower than my heat pumps minimum speed. Hence, the flow rate capabilities are also significantly oversized. Originally I had my Vaillant set to full pump speed, which in my system translated to around 28 l/min. I dropped pump speed to 20 l/min, which is a bit above the minimum by lowering the max. remaining head setting. This drops pump power from 93 to 46 W, approximately halving it. Based on my simple model but using the actually recorded pump powers, COP (during compressor on time) would increase from 4.43 to 4.65 - around 5%. Interestingly, I didn’t even raise my flow temperatures and didn’t experience any appreciable drop in house temperature. The required flow temperature increase would be around 0.2 K, which is below the granularity of Vaillant’s controls. So probably the house got ever so slightly cooler, but noone noticed or cares ![]() .
.
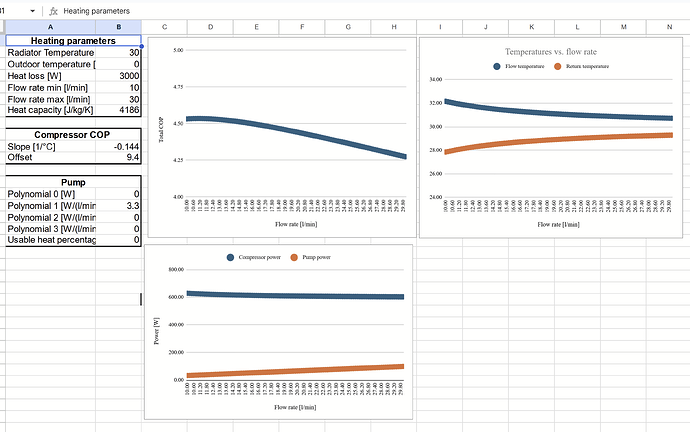
I have uploaded my excel sheet to Google Sheets if anyone wants to play with their own values. It should be pretty much self explanatory. For the pump electrical use, four polynomial coefficients can be entered to approximate power vs flow rate. The percentage of pump power usable as heat can also be set.