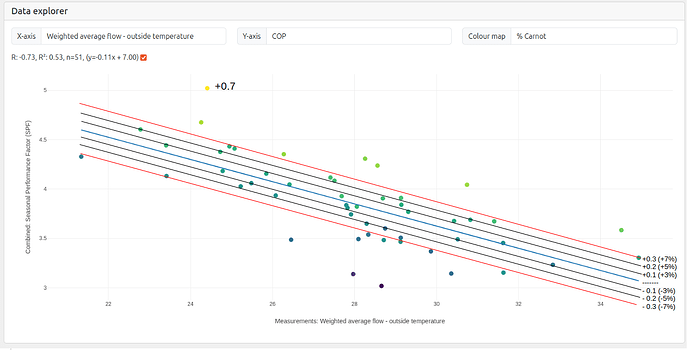
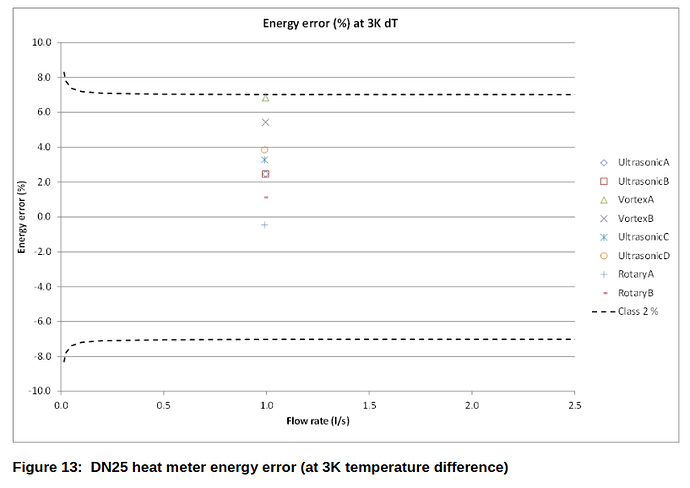
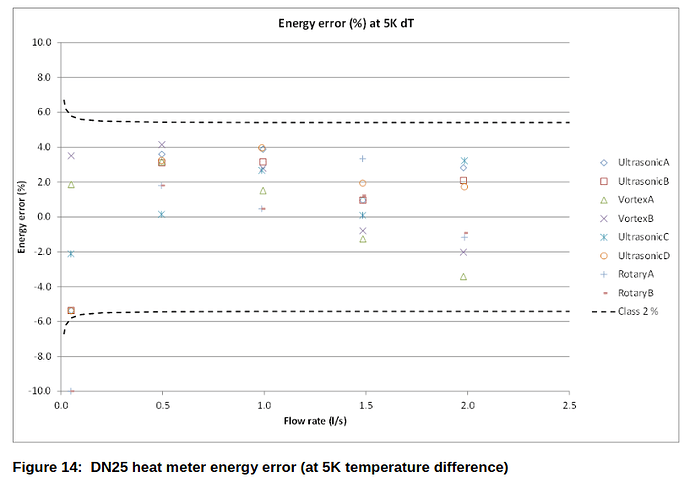
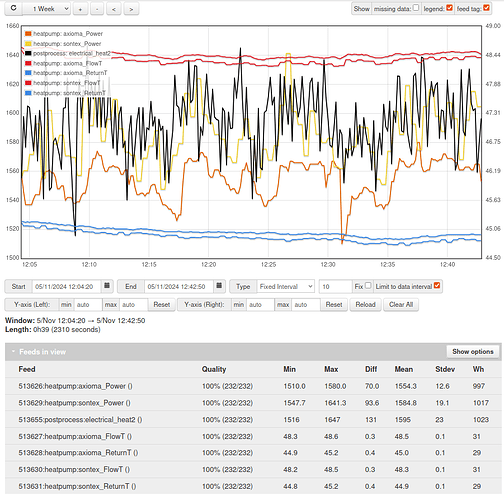
OpenEnergyMonitor test bench
We wanted to get a better understanding of the accuracy of heat meters in practice ourselves and so decided to build a test bench in our office. Here are a few pictures of the test bench, it consists of an inline electric element, a circulation pump and expansion vessel, two heat meters and a couple of 1200x600 K2 radiators.
We used radiators as a load rather than a big volume of water so that we could run the system at steady state conditions in order to avoid calculation complexity with heating of the water volume and system components themselves.
The inline electric element is driven by an MyEnergi Eddie PV diverter that we can use to set different power levels. We monitor both electrical input to the diverter and electrical output using both an SDM630 and EmonPi2, we also monitor the power used by the circulation pump.
Insulated in order to minimise heat loss between return and flow temperature sensor on the inline meter side of the heat meters: Bubble wrap used for part of this for quick configuration changes.
A later configuration with longer straight sections before the meters, please excuse the presentation 
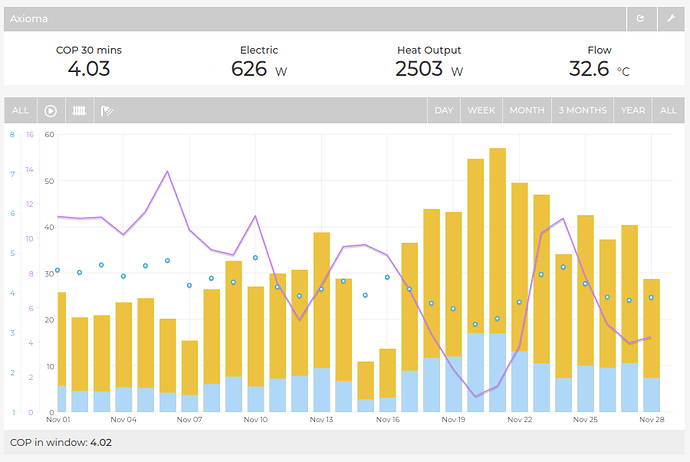
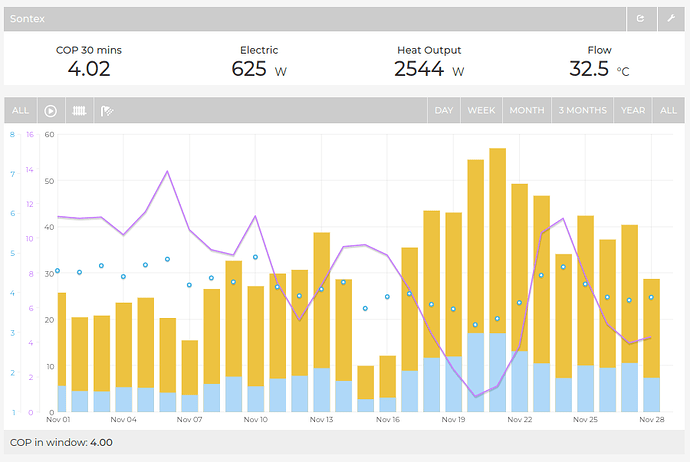
The data coming out of this typically looks like this.
-
We can see the flow and return temperatures rise at the beginning of this test period as we heat up the system volume. The electrical element (black line) was ran at full power at the start in order to get up to a reasonably high system temperature.
Note: We can see a relatively large error here between the electrical element input and the heat registered on the heat meters, most of this missing heat is heat used to heat up the primary volume of water and copper pipes, electrical element etc before the heat meter - this is why tests at constant temperature are so important.
-
The heat input is then reduced to a level that will keep the system at steady state using the Eddie programmable power levels.
-
We then select a period where the flow and return temperatures are as stable and flat as possible and take a set of averaged measurements across the period. In this particular example we took a set of measurements between 05/11/2024 12:04:20 and 05/11/2024 12:42:50 an average of about 230 datapoints per feed.
-
Zooming in on this section we see the following:
-
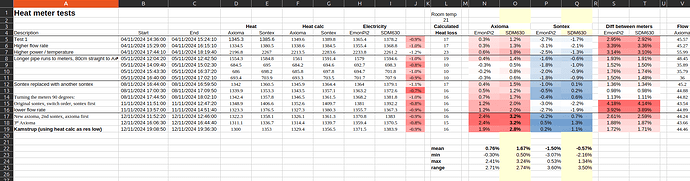
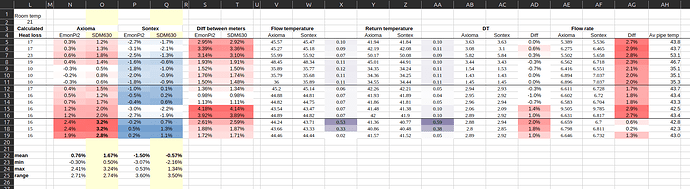
Heat input from the electrical element and central heating pump (~14W) in black. Measured heat output by the Sontex 789 under test in yellow. Measured heat output by the Axioma in orange.
-
The Sontex is on the face of it under-reading by 0.6%, the Axioma is a bit lower, under-reading by 2.6%, but we have not accounted for heat lost from the pipework, electric heater body and pump body prior to the heat meter yet.
Estimating heat loss prior to heat meter
Estimating heat loss to the room between flow and return temperature sensor’s, heat lost through insulated pipe sections.
There is about 2.8m of insulated pipework including 10mm insulation surrounding 15mm pipework, and a range of thickness around the pump and immersion heater ranging from 5mm to 15mm. Insulation work is not perfect, there are small sections of exposed pipework around some of the bends and clips.
If we assumed a continuous 2.8m length of 15mm pipework with 10mm insulation.
Q = 2 π * k * (T_fluid - T_room) / ln(ro / ri)
k = 0.035W/m2.K
T_fluid = 43.5 C
T_room = 21.0 C
ro = 0.0075m (outer radius of pipe 15mm / 2)
ri = 0.0175m (outer radius of insulation ro + 10mm)
Q = 5.84 W/m
Heat loss = ~2.8m x 5.8 W/m = ~16W
A section at 5mm insulation would be 9.7W/m and a section at 15mm insulation about 4.5 W/m.
There about 1m between the first heat meter and the second heat meter but insulation is thicker here. There’s also about 0.8m out of the 2.8m in 22mm pipe with 13mm insulation, heat lost from this section could be 6.3 W/m. I have assumed an average of about 5.8 W/m or DT x 0.26 W/m.K as a temperature dependent simplification.
Subtracting heat lost before the heat meter
For the example test period above the mean water temperature of the pipe was 46.7C and the room was 22C. The heat lost before the heat meter may therefore have been about 18W.
Subtracting this heat loss from the heat input 1595W - 18W = 1577W. The Sontex would now be over-reading by 0.5% and the Axioma would be under-reading by 1.4%. That’s a very respectable margin of error. 1.4% is equivalent to ±0.05 COP.
The next post provides results from a wider range of tests that we have performed.