perform clustering of appliances in the P/Q plane (real power vs reactive power domain)
You might want to confirm exactly what they’re referring to when they say “reactive power”. Once there are harmonics in the current signal (and there always will be assuming you have plenty of switch mode power supplies in your load mix), “reactive power” becomes a bit of an overloaded term.
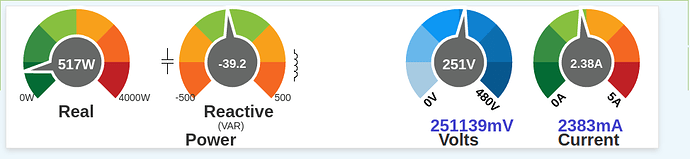
Here’s what my energy monitor reports for my GPO1 circuit (general purpose outlets, aka power-points):
At the time the loads were a good mix of electronics (computers, modems, printers, TVs, amplifiers, PVRs, lab equipment etc.) and the power factor is about 0.86. The first thing to notice is that the power triangle is broken: 5172 + 39.22 is way less than (251 x 2.38)2. What’s not shown is the distortion power which was 298.9 VAR at the time. Note that 5172 + 39.22 + 298.92 does equal (251 x 2.38)2Once there are harmonics involved, Apparent Power (which is always Vrms * Irms) becomes the sum of three orthogonal vectors: Real, Reactive and Distortion as shown in this diagram: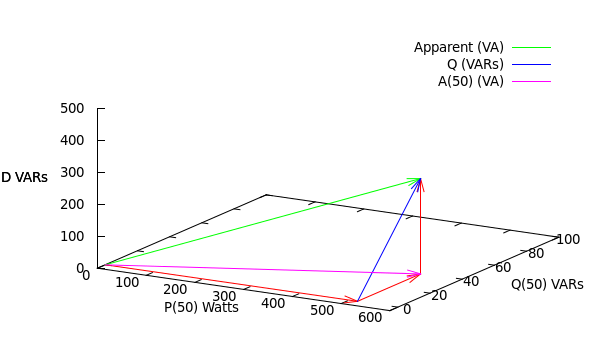
The three Red vectors are the raw ingredients: Real, Reactive and Distortion respectively, that add together to give Apparent Power (Green). I’ve labelled the Real axis P(50), the Reactive axis Q(50) and the Distortion axis D.
A useful mental simplification at this stage is to assume your V signal is a pure 50Hz sinewave and that your I signal has plenty of harmonics in it (we can add in the minor complication of small harmonics in V later1). When you multiply rapidly sampled V*I samples together like emonlib does (and in my case the energy IC does) you get Real Power (517W in this case). Now if you delay the V signal by 90o and multiply that by the I signal, you’ll get Reactive Power (-39.2VAR in this case).
In both calculations you’ve extracted just the 50Hz component out of the I signal, because the 50Hz V sine wave is orthogonal to a 100Hz sine wave (and to a 150Hz sine wave etc.); their dot product will always be zero. So all those harmonics in I will never show up in either of those two calculations and that’s why I’ve labelled those axes P(50) and Q(50). But those harmonics do show up in Irms (and hence Apparent Power) and so the two dimensional power triangle is broken. Distortion Power comes to the rescue and makes up the difference. Unlike the other two, Distortion Power can have no sign (or phase) because there’s no V at those frequencies to compare it against.
The two methods Robert mentioned: delay V by 90o or use Pythagoras on Apparent Power and Real Power will give you two very different results. The first method gives you the second Red vector (Q50) and the second method gives you the Blue vector. They’ll only be equal when the third Red vector is 0, i.e. there is no distortion in I, i.e. I is a pure sine wave.
If you’re trying to distinguish between your TV coming on and your computer coming on it may well be that the most distinguishing factors are in the harmonics in I. If you just use P(50) and Q(50) you’ll miss all that detail. I’m pretty sure the smappee product do their cluster analysis on a vector of harmonics in I (I can’t remember how high they go, but they used to expose it all on one of their debug pages).
- In reality your V signal will be slightly distorted. Rather than being a pure sine wave it often shows up with a slight flat-top. The measurements above (517, -39.2 and 298.9) were all true measurements, i.e. they took no short-cuts and made no assumptions about the purity of the V signal. So long as you do the V*I calculation, you’ll pick up the true measurements. The “error” introduced by the simplification above is simply one of labelling. P(50) and Q(50) become slight misnomers in the case where V isn’t a pure sine wave. The measurements (517W and -39.2VAR above) will be correct as per the IEEE definition, but they won’t strictly be just the 50Hz component. They’ll be primarily the 50Hz component, plus a bit of what otherwise would have got classified as Distortion Power. Some of that Distortion Power leaks into the Real and Reactive Power calculations as the harmonics in I find some harmonics in V to multiply against.