Great post @SarahH!
I can add a bit to this discussion since I have worked a lot on this topic the past year.
There is a very concise way to describe the thermal dynamics of a building using something called a lumped RC network. In literature you will find hundreds of papers that adopt this method in their work.
If you’re interested, the following papers are fantastic:
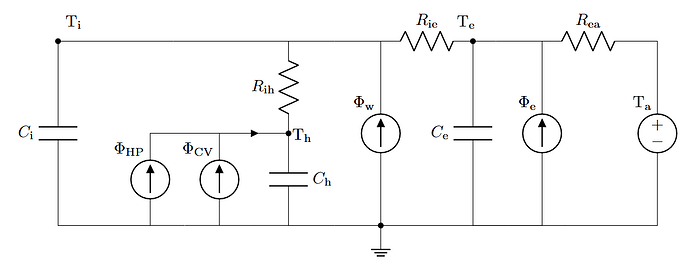
The basic idea is to model a building as a collection of thermal capacitors that store heat and thermal resistors that conduct heat. Heat can be added to the system by heat pumps, boilers, solar thermal gains, etc. Graphically that looks like this:
I added here nodes for the interior, the envelope, the emission system and ofcourse the ambient temperature. If you’ve ever worked with electronics this should look familiar to you. Whether you’re modelling voltage and current or temperature and heat flow, the equations are exactly the same!
We can find them by using the formula for conservation of energy, which means the flows going into a node must equal the flows going out of a node:
\begin{align}
\sum\Phi_{\mathrm{in}} &= \sum\Phi_{\mathrm{out}}
\end{align}
Where \Phi is heat flow in kW. Applying that to every temperature node gives you a system of differential equations:
\begin{align}
C_\mathrm{i}dT_\mathrm{i} =& \Phi_{\mathrm{w}}(t) + \frac{T_{\mathrm{h}}(t) - T_{\mathrm{i}}(t)}{R_{\mathrm{ih}}} + \frac{T_{\mathrm{e}}(t) - T_{\mathrm{i}}(t)}{R_{\mathrm{ie}}} \\
C_\mathrm{e}dT_\mathrm{e} =& \Phi_{\mathrm{e}}(t) + \frac{T_{\mathrm{a}}(t) - T_{\mathrm{e}}(t)}{R_{\mathrm{ea}}} + \frac{T_{\mathrm{i}}(t) - T_{\mathrm{e}}(t)}{R_{\mathrm{ie}}} \\
C_\mathrm{h}dT_\mathrm{h} =& \Phi_{\mathrm{CV}}(t) + \Phi_{\mathrm{HP}}(t) + \frac{T_{\mathrm{i}}(t) - T_{\mathrm{h}}(t)}{R_{\mathrm{ih}}}
\end{align}
I’ve summarized the meaning of the units in a table:
| Symbol |
Physical Interpretation |
Unit |
| C_\mathrm{i} |
Thermal mass of the building interior. |
kWh/C |
| C_\mathrm{e} |
Thermal mass of walls, floor and envelope. |
kWh/C |
| C_\mathrm{h} |
Thermal mass of the heat emission system. |
kWh/C |
| R_\mathrm{ih} |
Thermal resistance between emission and supply. |
C/kW |
| R_\mathrm{ea} |
House envelope insulation or air barrier. |
C/kW |
| R_\mathrm{ie} |
Insulation between interior and envelope. |
C/kW |
| R_\mathrm{ia} |
Direct leakage from the interior to outside. |
C/kW |
What can you do with this information? Well you can use it to answer the question whether roomstat setback is worth it or not, by directly using physics. You can also use this to build controllers, optimize your heating to variable rates, etc. For that part you also need to write more math and specify a controller, maybe I’ll write about that some other time